استفاده از بسط در رفع ابهام حدود | از بسط تیلور تا مک‌لورین

در ابتدای مسیر یادگیری حد، یک ابهام معروف همیشه خودش را نشان می‌دهد: حدود صفر صفر. همان جایی که وقتی مقدار را جای‌گذاری می‌کنی، هم صورت صفر می‌شود و هم مخرج؛ و عملاً چیزی دستت را نمی‌گیرد. اینجاست که استفاده از بسط در رفع ابهام حدود به‌عنوان یک ابزار نجات‌بخش وارد می‌شود. اگر تا امروز بسط تیلور یا بسط مک‌لورین برایت فقط یک فرمول حفظی بوده، این مقاله قرار است نگاهت را عوض کند.

🔗 لینک داخلی (شروع مقاله):
برای دسترسی به آموزش‌های بیشتر ریاضی و حد، می‌توانی از ابتدای کار به صفحه اصلی سایت ما سر بزنی:
https://fahmyar.ir

در ادامه، قدم‌به‌قدم و با زبان خودمانی اما دقیق، می‌بینیم که چطور بسط‌ها واقعاً به رفع ابهام حدود صفر صفر کمک می‌کنند، کِی باید از آن‌ها استفاده کرد، و چطور اشتباه نرویم.

---

ابهام حد صفر صفر دقیقاً یعنی چه؟

وقتی در محاسبه حد به حالتی می‌رسیم که با جای‌گذاری مستقیم، هم صورت و هم مخرج صفر می‌شوند، می‌گوییم با ابهام صفر بر صفر مواجه‌ایم. این حالت به‌خودیِ‌خود نه جواب را صفر می‌کند و نه بی‌نهایت؛ بلکه یعنی «اطلاعات کافی نداریم».

نکته مهم اینجاست:
ابهام صفر صفر یک مشکل محاسباتی نیست، بلکه یک علامت هشدار مفهومی است. یعنی باید رفتار تابع را نزدیک نقطه بررسی کنیم، نه فقط مقدارش را در همان نقطه.

---

چرا بسط‌ها در رفع ابهام حدود جواب می‌دهند؟

ایده اصلی بسیار ساده است، هرچند در ظاهر رسمی به نظر می‌رسد. وقتی تابعی نزدیک یک نقطه (مثلاً صفر) رفتار پیچیده‌ای دارد، ما آن را به کمک بسط تیلور یا مک‌لورین به یک چندجمله‌ای ساده‌تر تبدیل می‌کنیم.

واقعاً فکرش را می‌کردی که سینوس و نمایی و لگاریتم را بتوان با چند جمله ساده جایگزین کرد؟ همین جایگزینی است که قفل حد را باز می‌کند.

به‌طور خلاصه:

• بسط‌ها رفتار تابع را نزدیک نقطه مورد نظر نشان می‌دهند.
• جملات مشترک صورت و مخرج حذف می‌شوند.
• ابهام صفر صفر از بین می‌رود و حد قابل محاسبه می‌شود.

---

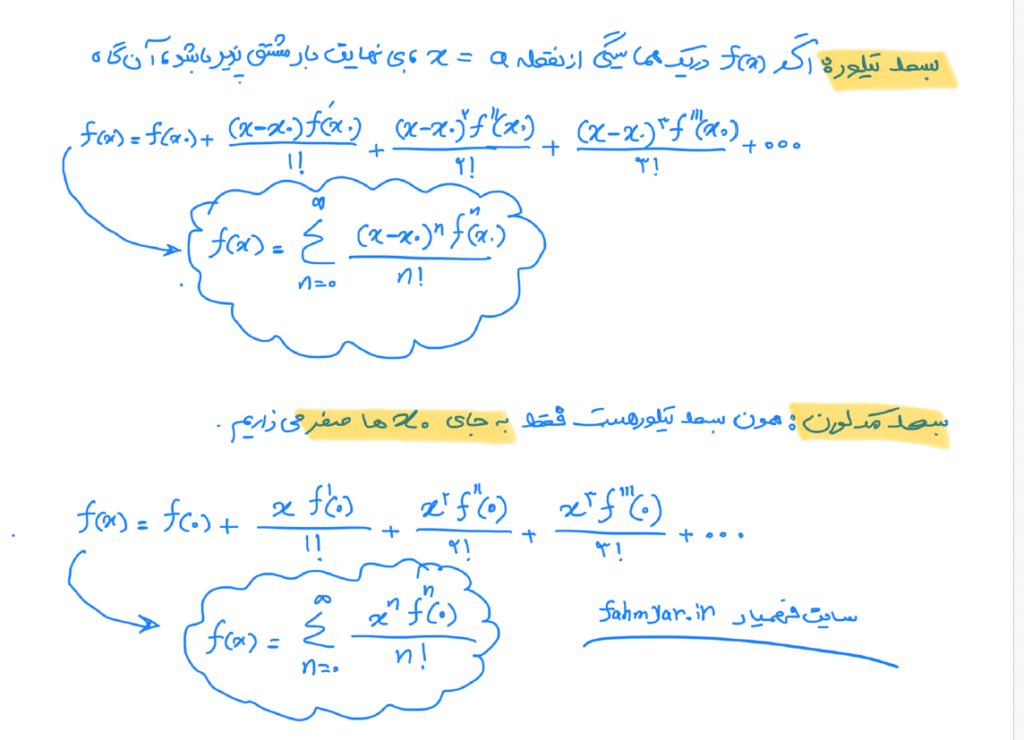
تفاوت بسط تیلور و بسط مک‌لورین در رفع ابهام حدود

خیلی‌ها این دو را قاطی می‌کنند، در حالی که تفاوت‌شان کوچک ولی مهم است.

نوع بسط	نقطه بسط	کاربرد رایج در حد
بسط مک‌لورین	حول $x=0$x=0	بسیار رایج در رفع ابهام حدود صفر صفر
بسط تیلور	حول $x=a$x=a	وقتی حد در عددی غیر از صفر باشد

اگر حد حول صفر باشد (که در ۸۰٪ سوال‌ها همین‌طور است)، معمولاً بسط مک‌لورین انتخاب اول است. اما اگر حد حول عددی مثل π یا ۱ تعریف شده باشد، بسط تیلور به دادت می‌رسد.

---

پرکاربردترین بسط‌ها برای رفع ابهام حدود صفر صفر

قبل از رفتن سراغ مثال، بهتر است چند بسط طلایی را بشناسیم. این‌ها همان‌هایی هستند که در امتحان و کنکور هم بارها استفاده می‌شوند.

تابع	بسط مک‌لورین (جملات مهم)
$\sin x$sinx	$x – \frac{x^3}{6} + \dots$x−6×3​+…
$\cos x$cosx	$1 – \frac{x^2}{2} + \dots$1−2×2​+…
$e^x$ex	$1 + x + \frac{x^2}{2} + \dots$1+x+2×2​+…
$\ln(1+x)$ln(1+x)	$x – \frac{x^2}{2} + \dots$x−2×2​+…

لازم نیست همه جملات را حفظ کنی؛ معمولاً دو یا سه جمله اول برای رفع ابهام حد کافی است.

---

مثال مفهومی: بسط چگونه ابهام صفر صفر را رفع می‌کند؟

فرض کن با چنین حدی روبه‌رو شده‌ای:$$\lim_{x \to 0} \frac{\sin x – x}{x^3}$$x→0lim​x3sinx−x​

در نگاه اول، جای‌گذاری مستقیم → صفر بر صفر. حالا بریم سراغ بسط مک‌لورین:$$\sin x = x – \frac{x^3}{6} + \dots$$sinx=x−6×3​+…

جای‌گذاری در صورت:$$(x – \frac{x^3}{6}) – x = -\frac{x^3}{6}$$(x−6×3​)−x=−6×3​

حالا کل کسر می‌شود:$$\frac{-\frac{x^3}{6}}{x^3} = -\frac{1}{6}$$x3−6×3​​=−61​

دیدی؟
ابهام صفر صفر کاملاً محو شد، بدون مشتق‌گیری و دردسر.

---

دانلود فایل PDF آموزش استفاده از بسط در رفع ابهام حدود

اگر ترجیح می‌دهی این مبحث را به‌صورت خلاصه، منظم و قابل چاپ مطالعه کنی، فایل PDF آموزش استفاده از بسط در رفع ابهام حدود صفر صفر برایت آماده شده است. این فایل مخصوص دانش‌آموزان و داوطلبانی طراحی شده که می‌خواهند بسط مک‌لورین و بسط تیلور را سریع، مفهومی و بدون حاشیه یاد بگیرند.

در این فایل آموزشی:

• مفهوم رفع ابهام حدود صفر صفر به زبان ساده توضیح داده شده
• بسط‌های پرکاربرد مک‌لورین و تیلور به‌صورت جمع‌بندی آمده‌اند
• مثال‌های حل‌شده‌ی امتحانی و کنکوری قرار داده شده
• نکات مهم و اشتباهات رایج دانش‌آموزان بررسی شده است

این PDF می‌تواند یک مرجع سریع قبل از امتحان یا مرور نهایی باشد و حتی برای مطالعه آفلاین هم کاملاً مناسب است.

🔽 دانلود فایل PDF آموزش استفاده از بسط در رفع ابهام حدود

---

چه زمانی استفاده از بسط بهترین انتخاب است؟

گاهی دانش‌آموزها می‌پرسند: «از کجا بفهمیم بسط بزنیم؟» سؤال خوبی است.

به‌صورت تجربی (و امتحانی!)، اگر:

• حد از نوع صفر صفر باشد
• شامل توابع مثلثاتی، نمایی یا لگاریتمی باشد
• فاکتورگیری ساده جواب ندهد

آن‌وقت استفاده از بسط در رفع ابهام حدود یکی از سریع‌ترین و مطمئن‌ترین راه‌هاست.

---

اشتباهات رایج هنگام استفاده از بسط تیلور و مک‌لورین

از تجربه‌ی تدریس (و حل تمرین با دانش‌آموزها) بگویم؛ این اشتباهات خیلی تکرار می‌شوند:

1. بسط زدن بیش از حد لازم و شلوغ کردن محاسبات
2. نگه نداشتن جملات هم‌مرتبه در صورت و مخرج
3. استفاده از بسط مک‌لورین وقتی حد حول صفر نیست
4. فراموش کردن اینکه هدف، حذف ابهام صفر صفر است نه نوشتن بسط کامل

اگر این‌ها را حواست باشد، کارت خیلی تمیز درمی‌آید.

---

بسط یا قاعده لوپیتال؟ کدام بهتر است؟

سؤال جذابی است، نه؟ واقعیت این است که هر دو ابزارند، اما فلسفه‌شان فرق می‌کند.

روش	مزیت	محدودیت
بسط تیلور / مک‌لورین	دید مفهومی، سریع، آموزشی	نیاز به شناخت بسط‌ها
لوپیتال	مکانیکی و ساده	مشتق‌گیری‌های پشت‌سرهم

در خیلی از کلاس‌ها، توصیه می‌شود اول بسط را امتحان کن؛ اگر جواب نداد، برو سراغ لوپیتال.

---

تجربه شخصی: چرا بسط را دوست دارم؟

صادقانه بگویم، وقتی اولین بار فهمیدم که می‌شود با چند جمله ساده رفتار یک تابع پیچیده را فهمید، واقعاً لذت بردم. بسط فقط یک ابزار حل سوال نیست؛ یک جور نگاه نزدیک‌بین به تابع است.
اصلاً فکرش را می‌کردی که پشت آن فرمول‌های خشک، چنین ایده قشنگی باشد؟

---

منابع معتبر برای مطالعه بیشتر

اگر دوست داری نگاه آکادمیک‌تری هم داشته باشی، این منبع خارجی بسیار معتبر است:

• Taylor Series – Wikipedia
  https://en.wikipedia.org/wiki/Taylor_series

(برای فهم عمیق‌تر مفهوم بسط تیلور و کاربردهایش در حد)

---

سوالات متداول

۱. آیا همیشه می‌توان از بسط برای رفع ابهام حدود صفر صفر استفاده کرد؟

نه همیشه، اما در بیشتر حدهایی که شامل توابع معروف هستند، بسط مک‌لورین یا تیلور بسیار مؤثر است.

۲. چند جمله از بسط کافی است؟

معمولاً تا جایی که ابهام صفر صفر از بین برود. اغلب دو یا سه جمله اول کفایت می‌کند.

۳. تفاوت بسط مک‌لورین و تیلور در امتحان چیست؟

مک‌لورین مخصوص حد حول صفر است؛ تیلور برای نقاط دیگر. انتخاب اشتباه نقطه بسط، جواب را خراب می‌کند.

۴. بسط بهتر است یا لوپیتال؟

اگر به درک مفهومی اهمیت می‌دهی، بسط. اگر فقط جواب می‌خواهی، لوپیتال هم کار راه‌انداز است.

۵. آیا بسط در کنکور هم کاربرد دارد؟

بله، بسیار. مخصوصاً در سوالات مفهومی حد و تحلیل رفتار تابع.